I’M sure I could have rounded that bend at twice the speed,” boasted an enthusiastic driver. I have a surprise for him: many factors influence the maximum speed a vehicle can round a specific bend, not only driver skill. Yes, driving prowess is important in controlling a vehicle at the critical limit, but engineering theory helps us determine those limits long before vehicles (or egos) are dented.
In keeping with this issue’s sporting flavour, I’ll highlight the cornering ability of some of the cars involved in this year’s Shootout in turn one of Killarney Racetrack to explain the factors at play. Luckily, we had racer Deon Joubert behind the wheel of each vehicle for consistency and to make such a comparison easy.
The theory
Tyres
Rubber is the primary influencer on a vehicle’s acceleration, control and stability. Tyres are also the sole contact patches. Grip, meanwhile, refers to the interaction of the rubber elements of the tyre and surface of the road at the contact patch. The rubber interacts with the road via various mechanisms, from mechanical gearing to the texture of the pavement and molecular adhesion to the surface. Fortunately, it’s unnecessary to understand the physical interaction, but only the associated forces. The tyre contact forces limit the accelerative performance of a vehicle in any direction.
Lateral forces
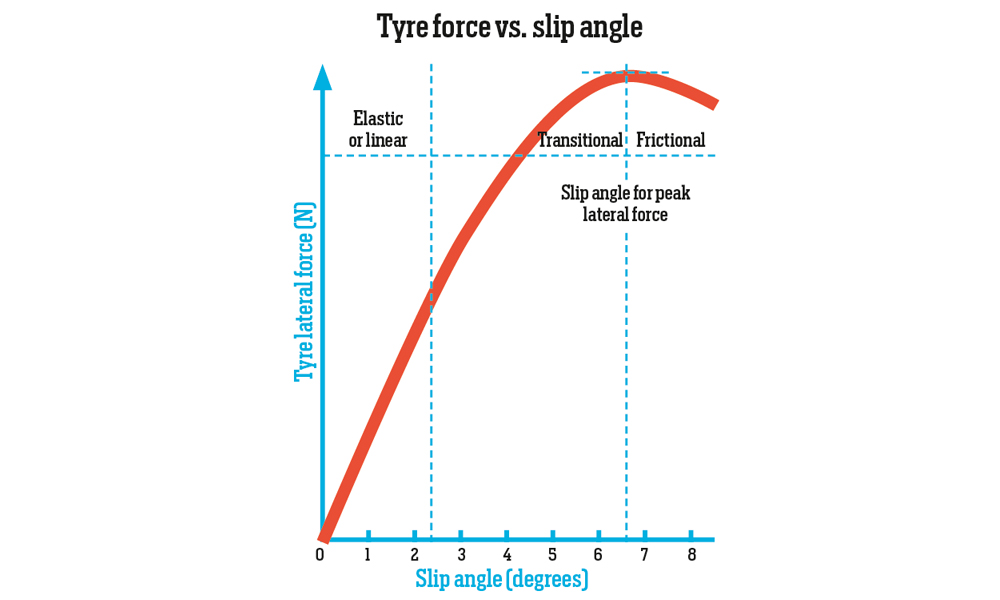
These forces, which allow a vehicle to round a bend, are generated at the contact patches. They are a result of the slip angle of a tyre (where the slip angle is the angle between the travelled direction of the tyre and the tyre heading). Therefore, even though there may be no steering angle on the rear wheels of a vehicle, there are still lateral forces generated at that end. Exceed the optimal slip angle and the lateral force drops off a steep curve (see below), leading to possible loss of vehicle control.
The vehicle-simulation model
Carmakers use advanced simulation software to predict a vehicle’s handling behaviour long before a prototype is developed for practical testing. A complex handling model includes the following parameters: exact vehicle dimensions and mass of components; position of the centre of gravity (COG); suspension geometry, including camber, castor and toe angles; spring and damper rates; steering geometry; and a complex tyre model (including construction and pressures). The latter is important as it is used to model the precise tyre interaction to the road surface during cornering, including contact patch deformation, in order to determine the exact lateral forces on each wheel. This method can also be used to compute the torque moment around the vertical axis that runs through the COG of a vehicle to determine the over-/understeer characteristics.
For the purposes of this elementary exercise, I have condensed the entire vehicle to a single tyre that has to cope with the full mass of the vehicle. This allows the calculation of maximum theoretical cornering speeds for a number of scenarios without taking specific handling characteristics into account.
The results
Corner radius
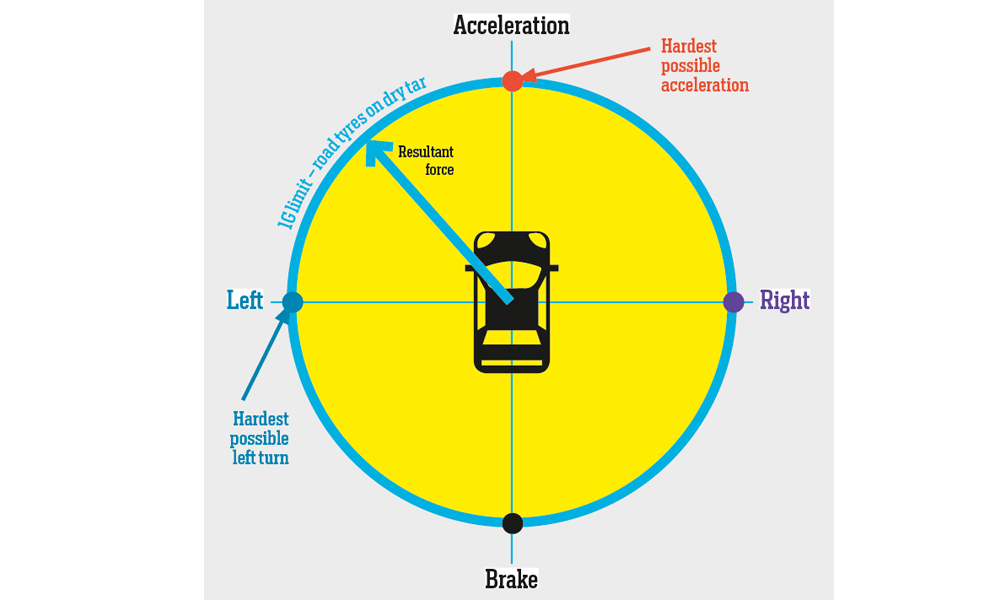
The radius at the apex of Killarney’s turn one is 66 metres. To calculate maximum apex speed, I chose a fixed coefficient of friction (typically one for a road tyre on dry tar) and varied the radius to calculate the maximum speeds at the grip limit. I assumed a lack of bank angle and no longitudinal acceleration at the apex, as last mentioned minimise the maximum lateral forces (see Friction circle concept).
Considering the table, the theoretical maximum speed at the apex of turn one is 91,6 km/h. This figure correlates with the speeds of the Mercedes-AMG GT S and Audi RS6 Avant Quattro (92 km/h), and Nissan GT-R Black Edition and Jaguar F-Type R Coupé AWD (93 km/h). It’s important to remember that doubling the radius does not double the possible vehicle speed.
Coefficient of grip
If we repeat the calculation, but keep the radius constant at 66 metres and vary the friction coefficient between the tyre and road, we see the influence of tyre grip on theoretical maximum apex speeds:
Clearly, tyre grip has a profound influence on potential maximum speed through a bend. The Mazda MX-5 2,0 recorded equal lowest maximum apex speed at turn one: 83 km/h. Although its tyre compound may have a lower friction coefficient than one, there are other factors that would have influenced ultimate grip that this elementary calculation can’t show, such as its soft suspension setup allowing too much body roll. This would have impacted the suspension geometry, which in turn would have distorted the tyre’s contact patch, effectively lowering the grip.
Downforce
Aerodynamic downforce effectively increases the normal force between the tyre and the road while vehicle mass stays the same. This allows for higher possible lateral acceleration and apex speeds, as shown in the table on the right.
This year’s Shootout competitors have very little aerodynamic downforce, as evidence by their cornering speeds. The last line in the table shows that a race slick plus 100% downforce equates to staggering theoretical cornering performance (159 km/h), explaining why F1 lap times are so impressive.
Why Do wider tyres have more grip?
Engineering theory states the coefficient of friction between two surfaces does not depend on contact area. The physical properties of tyres make them different. When a tyre starts to skid on dry tar, it leaves behind a black line. This means that the rubber isn’t slipping on the tar, but rather that a shearing force strips a thin layer of rubber from the tyre carcass. A larger tyre spreads this shearing force over a wider area, allowing the rubber to stay intact and so increasing grip. A wider tyre also aids stability during cornering.
Friction-circle concept
Maximum force can be generated in only one direction. Therefore, the maximum lateral cornering force occurs at the apex of a corner when the driver is neither on the accelerator, nor the brakes. A combination of braking and cornering lowers the lateral force. The fastest way round a corner is to apply maximum braking in a straight line. As the vehicle turns in and the lateral forces build, the driver bleeds off the brakes until the car reaches the apex. After the apex, the driver gets back on the throttle to use the increasing longitudinal grip for acceleration just as the lateral forces diminish when the corner opens. The best driver will always stay on the outer edge of the friction circle around a lap of a circuit, bar power limitations.
Basic formulas
To calculate the maximum possible vehicle speed round a bend, we need:
F = ma (Newton’s second law of motion)
where F is the force (N), m is the vehicle mass (kg) and a is the acceleration (m/s2)
Centripetal acceleration = V2/r
where V is the vehicle speed and r is the radius of the turn.
Therefore, the centripetal force on a vehicle is
Fcentripetal = m x V2/r
Where Fcentripetal = µmg (from tyre graphic at maximum grip)
Vehicle speed (V) is now the only unknown and can be calculated.
-Written by CAR’s technical editor, Nicol Louw